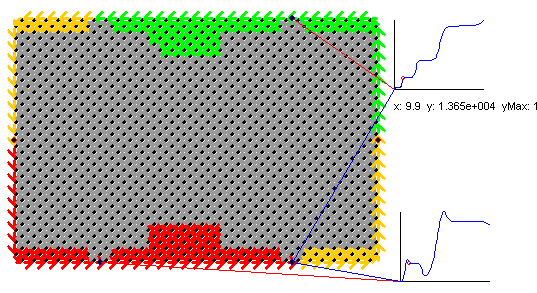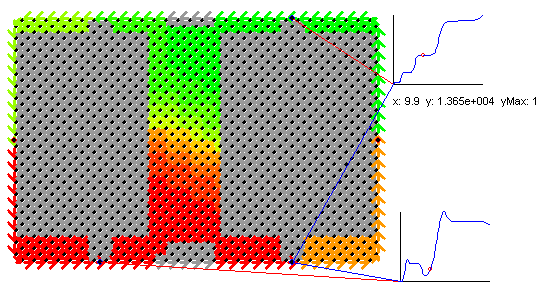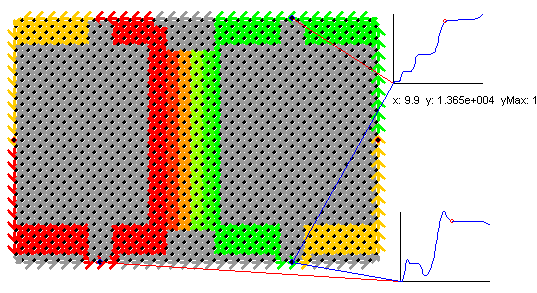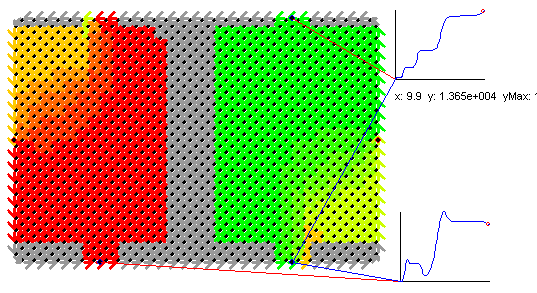
In this example special situations occur if the fillingfator outside the gate is n = 4 and n = 2 because in this cases the fillingfactor below the gate gets n_G = 2 and  n_G =1 respectively. This means for n = 4 two edge channels get transmitted through the gate and 2 edge channels get reflected. In the case n = 2 one edge channel gets transmitted and one reflected. The simulation shows the potential distribution in the second Landau level while the magnetic field sweeps in a way that the fillingfactor n changes from above n = 4 to n = 2. This means that at the beginning of the sweep the 2nd Landau level should create a transmitted EC while at the end it should create a reflected EC.  The Hall resistance and the longitudinal resistance are shown on the right. The actual position of the magnetic field is spotted by the red circle on the curves. According to the Landauer-Büttiker formalism R_xx and R_xy get identical, if the ration between reflection and transmission is one. This is the case if n = 4 and if  n = 2, where therefore R_xx  also forms plateaus like R_xy . According to this the n = 4 plateau and the n = 2 plateau are reproduced also by R_xx . In the intermediate regime the gated region performs a transition to the insulating state, which can be seen in the change of the potential gradient from the transvers to the the longitudinal direction. This behavior can be also seen like a HI-transition which partially takes place below the gate in the 2nd LL: