Wide parabolic quantum wells (WPQW) can be used to study a continuous transition from a 2D- to a 3D- electron system [1]. Recent investigations of PbTe WPQW’s have shown strong, reproducible fluctuation [2]. The explanation is based on the idea, that two electron systems in different valleys of the bandstructure contribute to transport. The one with the small effective mass is expected to build a 2D-like system which can form edge channels (EC) while the second one with the large mass is expected to lead to a 3D-like system [3].
Systematic experiments with different sample geometry and doping levels of the electron channel have been performed.

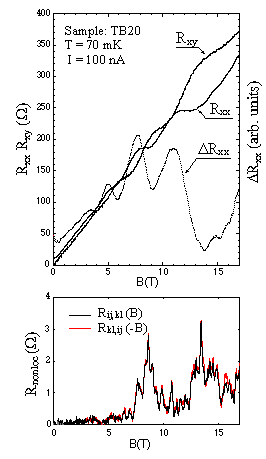
Fig.1: Magneto transport data of sample TB20.
Fig.1 shows Rxx, Rxy and non-local data for the case of a high bulk doping level. In addition, Rxx is also shown after subtracting the linear back ground (labelled deltaRxx). Bulk-Shubnikov de Haas (SdH) oscillations can be observed up to B=15 T. There can be found a striking similarity with the quantum Hall effect (QHE): (i) There are onsets of plateaux in Rxy which corresponds to minima in Rxx (deltaRxx). (ii) The maxima in Rxx (deltaRxx) appear in the regime of maximal slope in Rxy. However, the "plateaux" correspond to bulk-SdH oscillations and therefore cannot be attributed to 2D- fillingfactors. As explained below, this is not in contradiction with the model ! The key- point of the model is that one has to consider the native potential fluctuations in the electron channel as a substantial part of the electron system. They are equal or even larger than the typical subband splitting. This causes intersections of the Fermi level (EF) with the Landau-subband levels and consequently magnetic bound states ("EC- loops") in the bulk region can be created. These provide the possibility for EC-backscattering via tunnelling across these loops. A small subband splitting at EF leads to a high "loop density" and thus to strong back scattering. This happens if EF crosses a bulk Landau level (LL). In this way we get a remarkable correspondence between a standard quantum Hall (QH) system and our WPQW-system: (i) In QH-systems EC-back scattering occurs if a LL crosses EF while in the WPQW EC-back scattering is maximal if EF crosses a bulk-LL. (ii) The energy range between bulk- LL’s in the WPQW corresponds to the energy range between 2D- LL’s in the QH-system. If EF is between LL’s in the 2D system, EC-backscattering is completely suppressed while it is just reduced if EF is between bulk LL’s in the WPQW-system . This is because the subband splitting is larger at energies well above the bulk LL’s [1] and consequently the loop density and thus back scattering is reduced in this regime. This is also evident from the non- local signal (Fig. 1): The minima of Rxx (deltaRxx) correspond to maxima of the non-local signal. (iii) The role of the localised states in the QH system is taken over by the 3D-like valley in the PbTe WPQW’s. However, the 3D- like system is not isolating and therefore the zeros in Rxx are missing and a linear slope is superimposed to Rxx instead [4]. Finally the non-local signal clearly satisfies the Onsager-Casimir relation for the complete pattern. This is another indication that the general non-local behaviour and the superimposed fluctuations have the same physical origin.
In summary we conclude that the physical mechanisms which lead to the QHE in ideal 2D systems dominate also the magneto transport properties of high mobility WPQW-systems. Consequently the experiments shown in Fig.1 can be seen as the first observation of a 3D-QHE in WPQW’s [5].
[1] J.Oswald et al. Surface Science 361/362, 525 (1996)
[2] J.Oswald et al. Proc. of 3rd Int. Symposium on "New Phenomena in Mesoscopic Structures", Hawaii, Dec. 4-8, 1995, Physica B 227, 360 (1996)
[3] J.Oswald et al. Proc. of 12th Int. Conf. on Appl. of High Magnetic Fields, Würzburg 1996, in print
[4] J.Oswald and G.Span, Semicond. Sci. Technol., in print
[5] J. Oswald et al. , Solid State Commun., in print