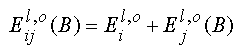
The basic idea of doping superlattices is to create a periodic band-edge modulation in real space without changes in the chemical composition [3,4]. By using a typical doping level of 1x10^17...3x10^17cm^-3 any potential modulation exceeding 10 meV leads to completely de- coupled potential wells in PbTe nipi- structures. The typical behaviour of such structures therefore can be investigated sufficiently by use of only a single period which in our case is a simple pnp- structure. In this pnp- structures the p- layers are designed to be non- depleted in order to screen the embedded n- channel from any influence from surface and interface states [5]. Selective contacts to the embedded n- channel are realised [6] in order to perform magneto transport experiments. The mobility in this selectively contacted structures is in the order of 3x10^5 ... 1x10^6 cm^2V^-1s^-1 at a temperature of T = 2.2K. The extremely high dielectric constant (500 - 1000) leads to wide quasi parabolic potential wells with a typical subband separation ranging from 1- 3 meV. A magnetic field perpendicular to the layers leads to a Landau level splitting which is large as compared to the subband splitting even at magnetic fields below B = 11 Tesla.
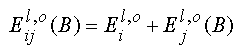
The subband energies are calculated selfconsistently by a numerical solution of the Schrödinger equation within the effective mass approximation. The energy level system consists of all Landau levels (LL's) sitting on each of the subband levels. Since in wide quantum wells the Landau level separation is much higher than the subband splitting, a picture which considers the Landau levels to be split by the subband quantization is more convenient. Therefore simply the Landau levels resulting from a 3D- calculation according to [7] are used (for more details on 3D-Landau levels of PbTe see also e.g. [8] or [9]). The modelling of the density of states (DOS) then is easily done by a superposition of individual Landau peaks with an appropriate broadening factor b. The broadening function in this approximation is assumed to be Gaussian. The total DOS as a function of energy E and magnetic field B then reads as follows:
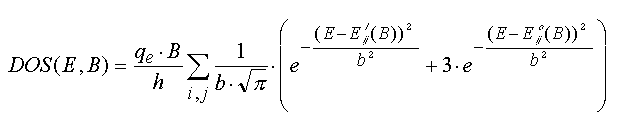
The numerical factor 3 in the second term in brackets accounts for the threefold degeneracy of the oblique valleys.
Fig. 1 shows the result of a model calculation for a sample with a carrier sheet density of n2D = 1.74x10^13cm^-2 and the background doping level in the electron channel of ND = 3x10^17cm^-3. The resulting shape of the potential near the bottom in the electron channel can be seen from the insert in Fig.1b. In Fig.1a the Fermi energy versus magnetic field is strongly influenced by the Landau levels of the subband ground states. This behaviour is the same like in 3D samples.
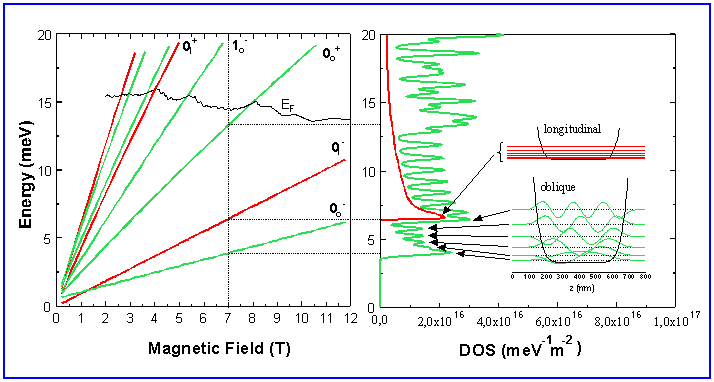
Fig 1. a) Landau levels of the subband ground states and Fermi energy versus magnetic field. b) density of states at B = 7 Tesla. Upper insert in b) potential and energy levels according to the longitudinal valley. Lower insert in b) potential, energy levels and wave functions according to the oblique valleys. The dashed curve in b) represents schematically the contribution of the longitudinal valleys.
For a basic understanding of the expected behaviour in magneto transport experiments one can consider two different idealized cases which will mix up in reality. One case is an ideal square potential and the second case is an ideal parabolic potential.
If we have an ideal square potential the subband energies depend on the square of the subband index. Therefore the lower subband levels are very close to each other and their associated Landau levels (of same Landau index) cause an overall enhancement of the density of states (DOS) near the subband ground state. The energy of the subband ground state is nearly identical to the position of the associated 3D - LL (LL of a three dimensional sample). At higher subband energies the subband levels are separated more and more and therefore a modulation of the DOS by the subband structure is more and more pronounced. In a parabolic potential well equally spaced subband levels are present. Therefore an ideal parabolic potential would not lead to an overall enhancement of the DOS at the position of the 3D - LL's. However, this idealized cases result from bare potentials and in real structures the situation will be different from both cases. The self consistent feedback of free electrons will change the potential as discussed in the following:
The effect of subband filling by adding electrons to an n-channel of a wide pnp-structure is limited by a Fermi energy which corresponds to the Fermi energy of bulk material at the same doping level. A further increase of the carrier sheet density therefore results in an increasing channel width and consequently a flat region in the middle of the electron channel is created. This behaviour starts in PbTe pnp structures which have a doping level of about 2x10^17cm^-3 at carrier sheet densities of about 6x10^12cm^-2. In this regime the subsequent filling of subbands by increasing the sheet carrier density is realised by a lowering of the subband energies while keeping the Fermi energy constant. The decrease of the subband energies happens by the increase of the channel width. In this way the subband structure turns more and more into the subband scheme of a square potential well. Consequently the lower part of the subband ladder looks like that of a square potential while the higher part will be dominated by the parabolic branches of the potential wells. For magneto transport experiments this means that there is an overall enhancement of the DOS at the energy position of the 3D-LL's and therefore also bulk like Shubnikov - de Haas (SdH) oscillations of the magneto resistance can be expected. At higher subband energies, which means the energy range between the 3D-LL's, a modulation of the DOS due to the subband structure can survive.
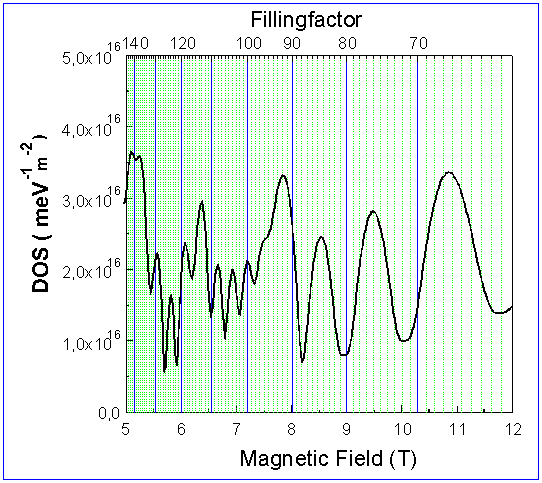
Fig.2: Density of states at the Fermi level versus magnetic field and filling factor according to Fig.1
The reason can be seen from Fig.1b. In this figure the DOS is plotted for a constant magnetic field of B = 7 Tesla. An overall enhancement of the DOS near the position of the 3D-LL's levels can be understood from the overlap of the DOS- peaks of the lowest Landau-subband states. The LL's of the subband ground states at B = 7 Tesla are marked by the dotted lines guiding from Fig.1a to Fig.1b. Because of the small subband separation in the longitudinal valley their contribution to the DOS is more or less a uniform background which is indicated schematically by the solid red line in Fig.1b.
[2] Dimmock J O 1971 The Physics of Semimetals and Narrow Band Semiconductors edited by Carter D L and Bate R T 405 (Pergamon, Oxford, 1971)
[3] Esaki L and Tsu R 1970 IBM J. Res. Dev. 14 61
[4] Döhler G H 1986 IEEE J. Quantum Electron. 22 1682
[5] Oswald J, Tranta B, Pippan M and Bauer G 1990 J. Opt. Quantum Electron. 22 243
[6] Oswald J and Pippan M 1993 Semicond. Sci. Technol. 8 435
[7] Burkhard H, Bauer G and Zawadzki W 1979 Phys. Rev. B 19 5149
[8] Oswald J, Goldberg B B, Bauer G and Stiles P J 1989 Phys. Rev. B 40 3032
[9] Oswald J, Pichler P, Goldberg B B and Bauer G 1994 Phys. Rev. B 49 17029