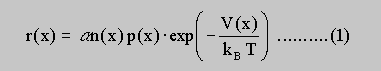
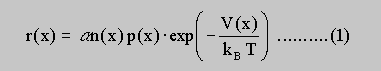
where x is the lateral coordinate of the linear shaped sample, n(x) and p(x) are the two dimensional carrier concentrations, V(x) is the potential modulation, T is the temperature and alpha is a constant prefactor. The generation-recombination kinetics is a dynamic process with a generation resulting in a current flowing from the n- to the p-layers (because of the internal electric fields) and a recombination resulting in a current from the p- to the n-layers. For the local treatment a leakage current density jB (x) is introduced with
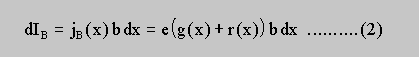
where IB(x) denotes the leakage current flowing in a sample area with length dx and width b from the n- to the p- layers and e is the elementary charge. This local ansatz does not only take into account the local dependence of the recombination rate r(x) but also allows the optical generation rate g(x) to be choosen inhomogeneously.
In many cases, especially in long period nipi structures, calculations within the space charge approximation will offer satisfactory results for the feedback of excess carriers on the potential modulation V: The effect of additional carriers nexc on the potential modulation V is described by use of a varying conducting channel which is assumed to have bulk-like carrier densities:
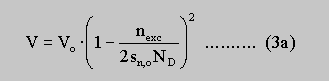
where nexc is the two dimensional excess carrier density which depends on the variation of the the conducting n- channel-width and thus on the reduction of the space charge region DELTAsn
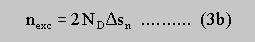
with
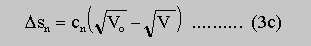
ND is the doping level of the n-layer and cn is a constant factor depending only on material parameters (Eq. 5). Vo denotes the potential modulation and sn,o the extension of the space charge region of the n-layer in thermal equilibrium. If a lateral constant current I is supplied via selective contacts to the n-layer a lateral voltage drop Vn(x) in the n-layer occurs. The current-voltage characteristics will not be linear because of the channel depletion effect but nevertheless Ohm's law will still hold locally
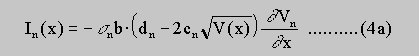
If a voltage drop in the n-layer occurs, the local leakage current IB (Eq.2) will not be zero, and a net leakage current flowing from the n-layer to the p-layers near the positive contact and a net leakage current from the p-layers to the n-layer near the negative contact will appear. This means that the current selectively supplied into the n-layer at the positive contact is more and more distributed to the p-layers and then, near the negative contact, redistributed to the n-layer again. Therefore in general the lateral current in the n-layer will not be constant (In not equal I) but is varying with the lateral coordinate x, denoted by In(x). Consequently an additional p-current Ip(x) will flow in the p-layers, and analogous to Eq. 4a one gets
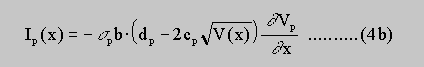
sigman , sigmap are the bulk conductivities of the n- and p-layers. The width of the conducting channel in the n- and p-layers results from the expression in parenthesis of Eq. 4a,b. According to the space charge approximation the constant factors cn and cp read as follows:
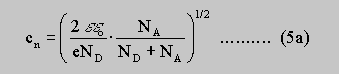
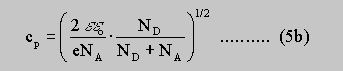
with the doping levels ND and NA in the n- and p-layers and the static DK epsilon. The potential modulation V(x) itself depends on the local values of Vn and Vp.
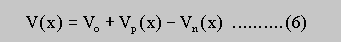
Any lateral distribution of the currents In(x) and Ip(x) which solves the above equations (1-6) has to satisfy boundery conditions at the selective contacts, which are assumed to be on either end of a linear sample: at the contacts the current is selectively supplied only into the n-layer and no current is flowing from the p-layers to the contacts directly. If also a break-through current has to be included (e.g. at higher voltages) only the boundery condition at the positive contact has to be modified in order to allow this kind of leakage current to flow between the p-layers and the positive n-contact. As a first approach, the magnitude of this break-through current is assumed to be exponentially dependent on the potential difference between the p-layers and the n-layer at the positive contact.