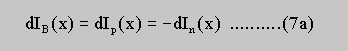
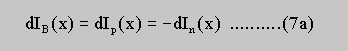
One way to find a solution for the distributions In(x) and Vn(x) on the basis of the equivalent circuit will be discussed briefly now:
For any constant sample current I we start the lateral evolution of the potential at the negative contact with some trial value V* of the potential modulation (0 < V* < = Vo ) and the current flowing only in the n-layer (boundery condition). This potential modulation V* at the left side of the first element causes a net leakage current IB1 (based on Eq. 2 ) between the layers and thus changes the currents In and Ip in the corresponding element according to Eqn. 7a. Considering an element of length DELTAx to be at position x, Eq. 7a can be rewritten as
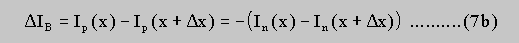
The "new" currents produce local voltage drops DELTAVn and DELTAVp at the local resistors Rn and Rp and cause a "new" potential modulation V at the right side of this element, which in turn determines the net leakage current DELTAIB in the next element. This procedure is repeated from the first (at the negative contact) to the last element (at the positive contact). Now the boundery condition at the positive contact is checked: Dependent on the deviation from the boundery condition the trial value V* of the potential odulation at the negative contact is varied, the procedure described above is repeated and the boundery condition is checked again. This iteration is continued until the boundery condition is sufficiently satisfied.
In this way the current and voltage distributions can be found for any arbitrary generation profile g(x). Performing the procedure for different constant currents allows to obtain the I(V)-characteristics.