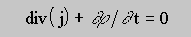
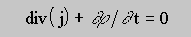
which includes also changes of the space charge rho. In addition to the discretization in space also a discretization in time has to be introduced. The solving algorithm now is different to the stationary case discussed before. There we used a mathematical trial-error algorithm, whereas the algorithm for time resolved solutions uses a physical "driving force", the continuity equation. Deviations from steady state conditions can arise e.g. from switching on some additional generation source. The resulting local changes of the space charge in time
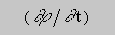
and hence the potential modulation then also cause changes of the currents in the n- and p-layers and therefore the current balance is destroyed
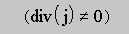
This mechanism itself is used for the numerical iterations in the following way:
The time resolved calculation starts from a steady state situation which is found by applying the algorithm discussed above . Then a generation source is switched on/off by an abrupt change of the generation g(x). In an experiment this is done by a laser pulse. For a single time step t to t+ DELTA t first a loop including the calculation
of the "new" net leakage currents of all discrete elements of the sample is carried out. Now the current bilance in the elements does not satisfy the steady state continuity equation, which leads to changes of the space charge in the element (figure ). For an element ranging from x to x+ DELTA x this changes of space charge DELTA Qn and DELTA Qp are
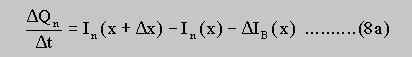
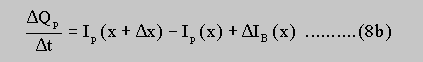
The effect of the additional charges DELTA Qn and DELTA Qp in the layers on the local potential modulation V(x) is treated within the space charge approximation as already mentioned above. The change of the values of the potential modulation is calculated within a loop which also runs over all elements. Now the modified potential modulation V(x) together with the boundery conditions is used to calculate the "new" lateral current distribution which is the basis for the next time step. These "lateral" and "temporal" loops are carried out until a new stationary equilibrium is reached and thus no further changes of space charge occur from one time step to the other: DELTA Qn=DELTA Qp=0.